Map of France

Population Perpezat



 Find a town, a zip code,
a department, a region... in France
I like Map-France.com !
 
 

Perpezat population statistics



Population of Perpezat was 380 inhabitants in 2007. You will find below a series of charts and statistical curves of population census of the town of Perpezat.
Population of Perpezat was 384 inhabitants in 1999, 377 inhabitants in 1990, 420 inhabitants in 1982, 454 inhabitants in 1975 and 519 inhabitants in 1968.

Area of Perpezat is 36,19 km² and has a population density of 10,50 inhabs/km².

Find statistics and informations of the population of nearby towns of Perpezat :
   - demography of Rochefort-Montagne : town located at 2.42 km
   - demography of Laqueuille : town located at 4.54 km
   - demography of Orcival : town located at 5.26 km
   - demography of Heume-l'Église : town located at 5.32 km
   - demography of Saint-Pierre-Roche : town located at 6.41 km
   - demography of Saint-Bonnet-près-Orcival : town located at 7.24 km
   - demography of Saint-Julien-Puy-Lavèze : town located at 8.03 km
   - demography of Vernines : town located at 8.19 km


See population statistics of the department prefecture of Puy-de-Dôme : Population of Clermont-Ferrand

See population statistics of other cities of Puy-de-Dôme : Puy-de-Dôme

Must see: housing of Perpezat, the road map of Perpezat, the photos of Perpezat, the map of Perpezat.

I like Perpezat !
   


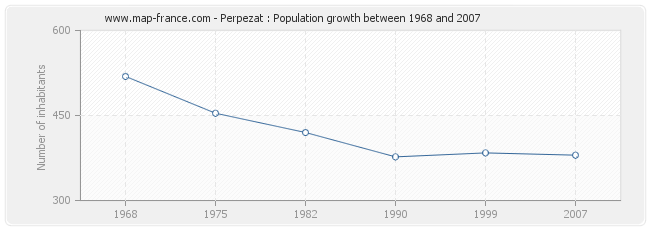
Historical data of the population of Perpezat from 1968 to 2007




Historical data of the population of Perpezat from 1968 to 2007 :

Population of Perpezat was 380 inhabitants in 2007, 384 inhabitants in 1999, 377 inhabitants in 1990, 420 inhabitants in 1982, 454 inhabitants in 1975 and 519 inhabitants in 1968.

This population Census of the town of Perpezat was made without duplicated data, which means that each Perpezat resident that have ties to another municipality is counted only once for the two municipalities.
Population Perpezat
Population Perpezat






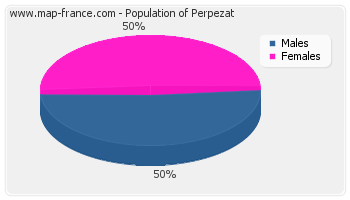
Population distribution of Perpezat by sexe



Population distribution of Perpezat by sexe :
- Men inhabitants Perpezat in 2007 were 191
- Women inhabitants in 2007 were 189

Sex distribution of population of Perpezat in 2007






Evolution of the population of Perpezat


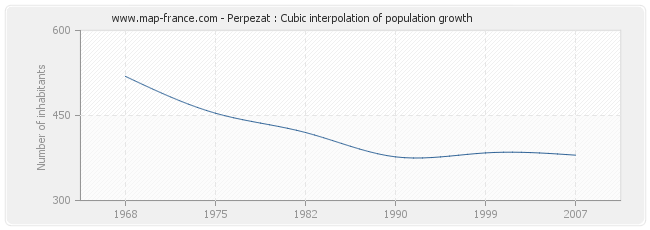
Population of Perpezat from 1968 to 2007 :

This curve shows the history of the population of Perpezat from 1968 to 2007 in cubic interpolation. This provides more precisely the population of the municipality of Perpezat the years where no census has been taken.

- Population of Perpezat in 2007 : 380 inhabitants
- Population of Perpezat in 1999 : 384 inhabitants
- Population of Perpezat in 1990 : 377 inhabitants
- Population of Perpezat in 1982 : 420 inhabitants
- Population of Perpezat in 1975 : 454 inhabitants
- Population of Perpezat in 1968 : 519 inhabitants
Perpezat : Cubic interpolation of population growth






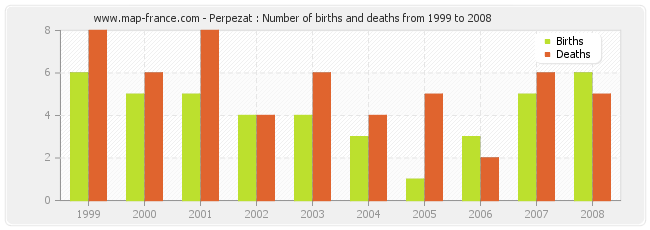
Perpezat : births and deaths



Perpezat : births and deaths from 1999 to 2008

- Perpezat in 2008 : 6 births and 5 deaths
- Perpezat in 2007 : 5 births and 6 deaths
- Perpezat in 2006 : 3 births and 2 deaths
- Perpezat in 2005 : 1 births and 5 deaths
- Perpezat in 2004 : 3 births and 4 deaths
- Perpezat in 2003 : 4 births and 6 deaths
- Perpezat in 2002 : 4 births and 4 deaths
- Perpezat in 2001 : 5 births and 8 deaths
- Perpezat in 2000 : 5 births and 6 deaths
- Perpezat in 1999 : 6 births and 8 deaths

 Perpezat : Number of births and deaths from 1999 to 2008



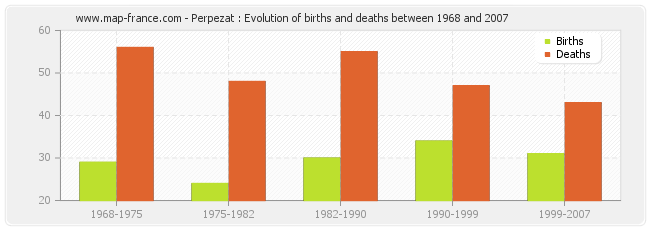
Perpezat : evolution of births and deaths from 1968 to 2007

- From 1999 and 2007 : 31 births and 43 deaths.
- From 1990 and 1999 : 34 births and 47 deaths.
- From 1982 and 1990 : 30 births and 55 deaths.
- From 1975 and 1982 : 24 births and 48 deaths.
- From 1968 and 1975 : 29 births and 56 deaths.

 Perpezat : Evolution of births and deaths between 1968 and 2007






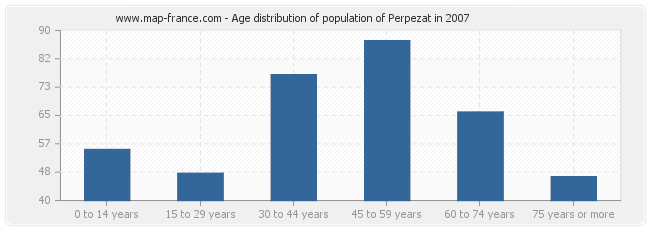
Distribution of the population of Perpezat by age



Distribution of the population of Perpezat by age in 2007 :

- Population of Perpezat from 0 to 14 years : 55 inhabitants
- Population of Perpezat from 15 to 29 years : 48 inhabitants
- Population of Perpezat from 30 to 44 years : 77 inhabitants
- Population of Perpezat from 45 to 59 years : 87 inhabitants
- Population of Perpezat from 60 to 74 years : 66 inhabitants
- Population of Perpezat from 75 years or more : 47 inhabitants
 Age distribution of population of Perpezat in 2007



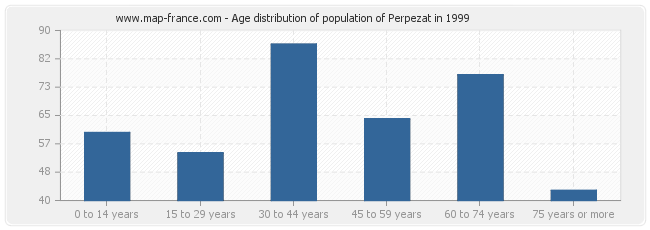
Distribution of the population of Perpezat by age in 1999 :

- Population of Perpezat from 0 to 14 years : 60 inhabitants
- Population of Perpezat from 15 to 29 years : 54 inhabitants
- Population of Perpezat from 30 to 44 years : 86 inhabitants
- Population of Perpezat from 45 to 59 years : 64 inhabitants
- Population of Perpezat from 60 to 74 years : 77 inhabitants
- Population of Perpezat from 75 years or more : 43 inhabitants
 Age distribution of population of Perpezat in 1999






Men population of Perpezat in 2007



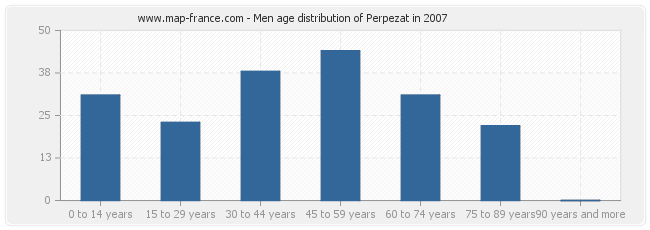
Men population distribution of Perpezat by age in 2007 :

- Perpezat men inhabitants from 0 to 14 years : 31
- Perpezat men inhabitants from 15 to 29 years : 23
- Perpezat men inhabitants from 30 to 44 years : 38
- Perpezat men inhabitants from 45 to 59 years : 44
- Perpezat men inhabitants from 60 to 74 years : 31
- Perpezat men inhabitants from 75 to 90 years : 22
- Perpezat men inhabitants of 90 years and more : 0
 Men age distribution of Perpezat in 2007



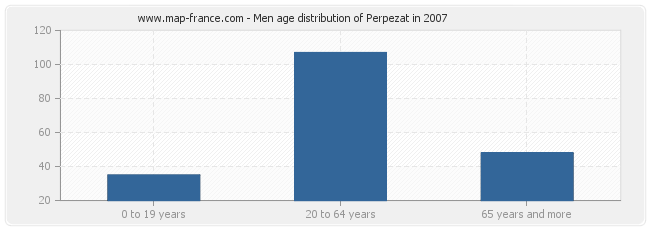
Men population distribution of Perpezat by age in 2007 :

- Perpezat men inhabitants from 0 to 19 years : 35
- Perpezat men inhabitants from 20 to 64 years : 107
- Perpezat men inhabitants of 65 years and more : 48
 Men age distribution of Perpezat in 2007






Population féminine of Perpezat in 2007



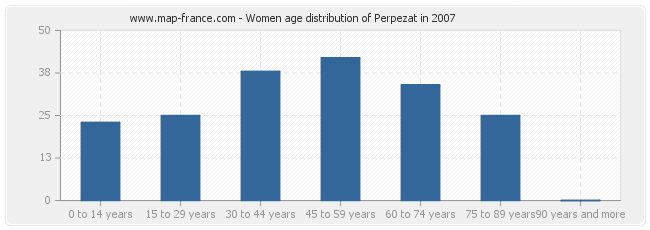
Women population distribution of Perpezat by age in 2007 :

- Perpezat women inhabitants from 0 to 14 years : 23
- Perpezat women inhabitants from 15 to 29 years : 25
- Perpezat women inhabitants from 30 to 44 years : 38
- Perpezat women inhabitants from 45 to 59 years : 42
- Perpezat women inhabitants from 60 to 74 years : 34
- Perpezat women inhabitants from 75 to 90 years : 25
- Perpezat women inhabitants of 90 years and more : 0
 Women age distribution of Perpezat in 2007



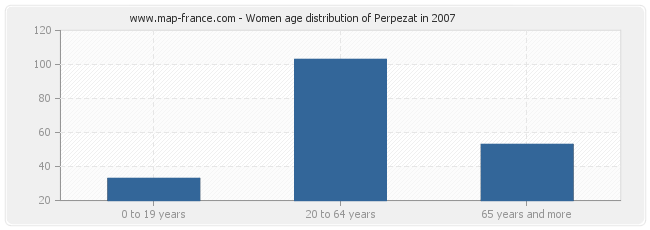
Women population distribution of Perpezat by age in 2007 :

- Perpezat women inhabitants from 0 to 19 years : 33
- Perpezat women inhabitants from 20 to 64 years : 103
- Perpezat women inhabitants of 65 years and more : 53

 Women age distribution of Perpezat in 2007






Other population statistics, maps, hotels of towns in france


Find the population data of another town, zip code, department, region, ...



Quick links Perpezat :






Back to the menus Map of France :







Make a link to this page of Perpezat with the following code :




Map of France | Regions | Departments | Cities | Partners | Terms | Contact