|
|
|
|
|
|
Teilhet population statistics
|
|
|
|
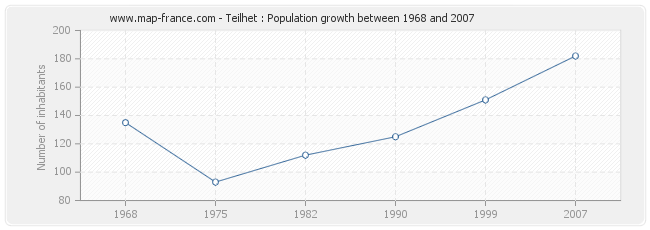
Historical data of the population of Teilhet from 1968 to 2007
Historical data of the population of Teilhet from 1968 to 2007 :
Population of Teilhet was 182 inhabitants in 2007, 151 inhabitants in 1999, 125 inhabitants in 1990, 112 inhabitants in 1982, 93 inhabitants in 1975 and 135 inhabitants in 1968.
This population Census of the town of Teilhet was made without duplicated data, which means that each Teilhet resident that have ties to another municipality is counted only once for the two municipalities.
|
Population Teilhet
|
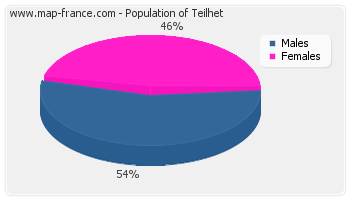
Population distribution of Teilhet by sexe
Population distribution of Teilhet by sexe :
- Men inhabitants Teilhet in 2007 were 99
- Women inhabitants in 2007 were 83
|
|
Evolution of the population of Teilhet
|
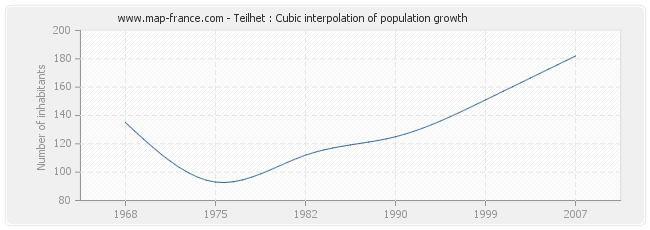
Population of Teilhet from 1968 to 2007 :
This curve shows the history of the population of Teilhet from 1968 to 2007 in cubic interpolation. This provides more precisely the population of the municipality of Teilhet the years where no census has been taken.
- Population of Teilhet in 2007 : 182 inhabitants
- Population of Teilhet in 1999 : 151 inhabitants
- Population of Teilhet in 1990 : 125 inhabitants
- Population of Teilhet in 1982 : 112 inhabitants
- Population of Teilhet in 1975 : 93 inhabitants
- Population of Teilhet in 1968 : 135 inhabitants
|
|
Teilhet : births and deaths
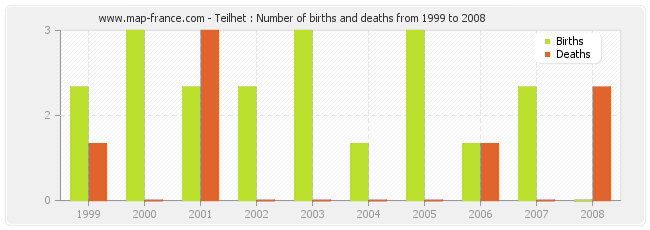
Teilhet : births and deaths from 1999 to 2008
- Teilhet in 2008 : 0 births and 2 deaths
- Teilhet in 2007 : 2 births and 0 deaths
- Teilhet in 2006 : 1 births and 1 deaths
- Teilhet in 2005 : 3 births and 0 deaths
- Teilhet in 2004 : 1 births and 0 deaths
- Teilhet in 2003 : 3 births and 0 deaths
- Teilhet in 2002 : 2 births and 0 deaths
- Teilhet in 2001 : 2 births and 3 deaths
- Teilhet in 2000 : 3 births and 0 deaths
- Teilhet in 1999 : 2 births and 1 deaths
|
|
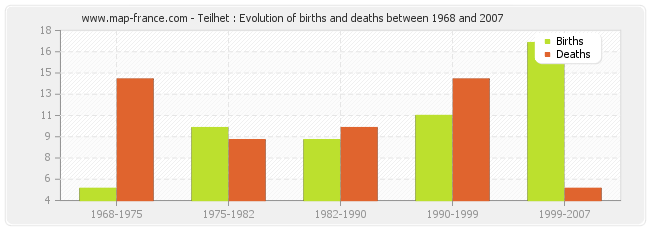
Teilhet : evolution of births and deaths from 1968 to 2007
- From 1999 and 2007 : 17 births and 5 deaths.
- From 1990 and 1999 : 11 births and 14 deaths.
- From 1982 and 1990 : 9 births and 10 deaths.
- From 1975 and 1982 : 10 births and 9 deaths.
- From 1968 and 1975 : 5 births and 14 deaths.
|
|
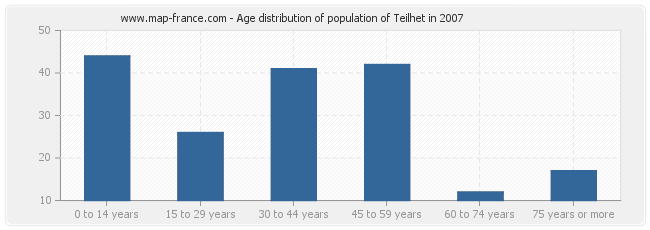
Distribution of the population of Teilhet by age
Distribution of the population of Teilhet by age in 2007 :
- Population of Teilhet from 0 to 14 years : 44 inhabitants
- Population of Teilhet from 15 to 29 years : 26 inhabitants
- Population of Teilhet from 30 to 44 years : 41 inhabitants
- Population of Teilhet from 45 to 59 years : 42 inhabitants
- Population of Teilhet from 60 to 74 years : 12 inhabitants
- Population of Teilhet from 75 years or more : 17 inhabitants
|
|
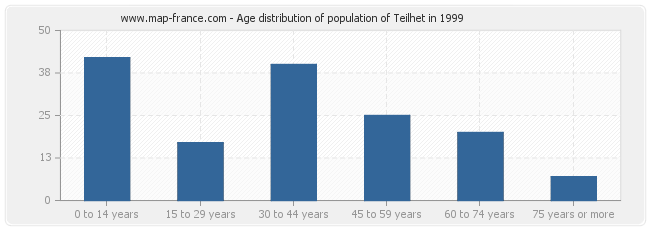
Distribution of the population of Teilhet by age in 1999 :
- Population of Teilhet from 0 to 14 years : 42 inhabitants
- Population of Teilhet from 15 to 29 years : 17 inhabitants
- Population of Teilhet from 30 to 44 years : 40 inhabitants
- Population of Teilhet from 45 to 59 years : 25 inhabitants
- Population of Teilhet from 60 to 74 years : 20 inhabitants
- Population of Teilhet from 75 years or more : 7 inhabitants
|
|
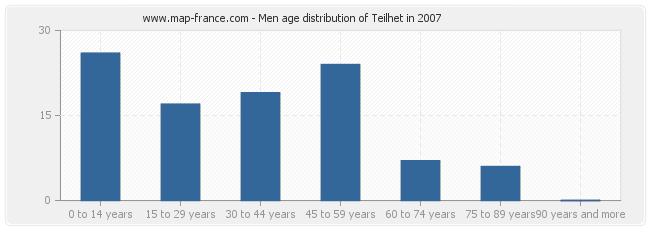
Men population of Teilhet in 2007
Men population distribution of Teilhet by age in 2007 :
- Teilhet men inhabitants from 0 to 14 years : 26
- Teilhet men inhabitants from 15 to 29 years : 17
- Teilhet men inhabitants from 30 to 44 years : 19
- Teilhet men inhabitants from 45 to 59 years : 24
- Teilhet men inhabitants from 60 to 74 years : 7
- Teilhet men inhabitants from 75 to 90 years : 6
- Teilhet men inhabitants of 90 years and more : 0
|
|
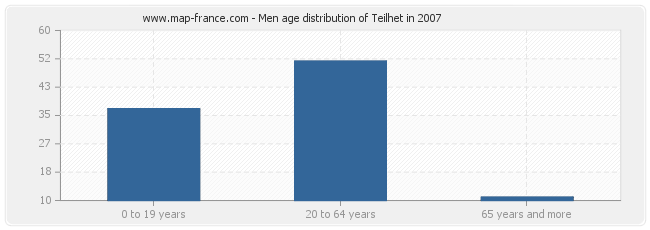
Men population distribution of Teilhet by age in 2007 :
- Teilhet men inhabitants from 0 to 19 years : 37
- Teilhet men inhabitants from 20 to 64 years : 51
- Teilhet men inhabitants of 65 years and more : 11
|
|
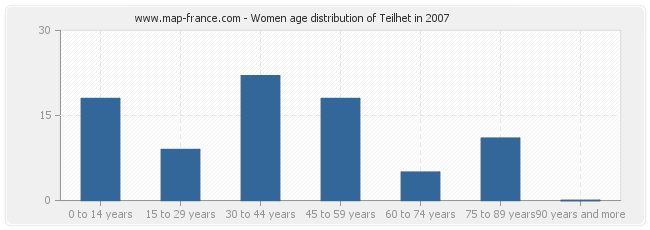
Population féminine of Teilhet in 2007
Women population distribution of Teilhet by age in 2007 :
- Teilhet women inhabitants from 0 to 14 years : 18
- Teilhet women inhabitants from 15 to 29 years : 9
- Teilhet women inhabitants from 30 to 44 years : 22
- Teilhet women inhabitants from 45 to 59 years : 18
- Teilhet women inhabitants from 60 to 74 years : 5
- Teilhet women inhabitants from 75 to 90 years : 11
- Teilhet women inhabitants of 90 years and more : 0
|
|
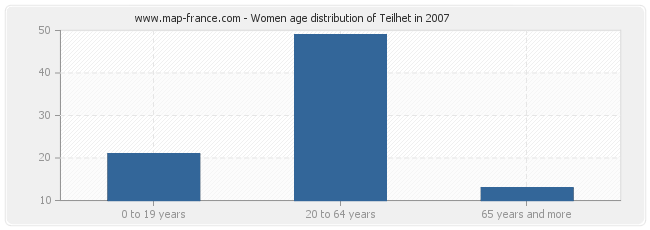
Women population distribution of Teilhet by age in 2007 :
- Teilhet women inhabitants from 0 to 19 years : 21
- Teilhet women inhabitants from 20 to 64 years : 49
- Teilhet women inhabitants of 65 years and more : 13
|
|
|
Other population statistics, maps, hotels of towns in france
Find the population data of another town, zip code, department, region, ...
Quick links Teilhet :
Back to the menus Map of France :
Make a link to this page of Teilhet with the following code :
|
|
Map of France | Regions | Departments | Cities | Partners | Terms | Contact
|